Neste tópico, apresentaremos um breve histórico acerca do desenvolvimento da Estatística, da Educação Estatística, além de aspectos relacionados às perspectivas teóricas de Educação Estatística.

Willcox (1938) cita cinco homens que têm a honra de serem, em momentos distintos, considerados os fundadores da Estatística: Hermann Conring, Gottfried Achenwall, Johann Peter Süssmilch, John Graunt e William Petty. Entretanto, a Achenwall é atribuída a criação da palavra "Estatística", variação de Staatenkunde e, posteriormente, Statistik, em alemão, que

consistia basicamente na descrição comparativa entre Estados – seus territórios, governos, economias e populações – a partir de uma perspectiva essencialmente empirista e qualitativa, que se aproximava mais de uma ciência política do que de uma ciência matemática. (SANTOS, 2016, p. 53)

A Estatística, enquanto área de conhecimento, é reconhecida autonomamente desde o século XVII, na Alemanha. No mesmo país surgiu o primeiro curso universitário de Estatística, em 1708, na Universidade de Jena. Entretanto, é importante perceber que há grande diferença entre a Staatenkunde alemã e os conhecimentos matemáticos precursores da Estatística moderna praticada na Inglaterra por John Graunt (1620 – 1674) e William Petty (1623 – 1683) (SANTOS, 2016). Ao primeiro pesa a primeira tentativa de, a partir de dados numéricos, se extrair conclusões, visto que em 1662 apresentou a compilação de nascimentos e mortes em Londres no período compreendido entre os anos 1604 e 1660, enquanto ao segundo, contemporâneo e continuador da obra de Graunt, cunhou o termo Aritmética Política, que consiste da "nova arte de raciocinar por meio de dados sobre fatos relacionados com o governo" (MEMÓRIA, 2004, p. 13). Com o desenvolvimento da Estatística Moderna, por volta do século XX, a Aritmética Política evoluiu para o que conhecemos na atualidade como Demografia.

Apesar da importância de Graunt e Petty, tivemos diversos nomes que influenciaram o avanço da Estatística, como os italianos Niccolò Fontana Tartaglia (1499 – 1557), Girolamo Cardano (1501 – 1576), seguidos por Galileu Galilei (1564 – 1642), os quais exploraram problemas de probabilidade relacionados aos jogos de dados. O suíço Jacob Bernoulli (1654 – 1705) expandiu tais conceitos, ao propor um modelo em que casos igualmente possíveis não fossem numeráveis. Além deles, podemos citar os franceses Abraham De Moivre (1667 – 1754), Pierre Simon, Marquês de Laplace (1749 – 1827), André Marie Legendre (1752 – 1833), o alemão Carl Friedrich Gauss (1777 – 1855), os ingleses Ronald Aylmer Fisher (1890 – 1962) e Karl Pearson (1857 – 1936) Entretanto, dois nomes foram relevantes para uma nova forma de compreender a Estatística: o belga Lambert Adolphe Jacques Quételet (1796 –1874) e o inglês Sir Francis Galton (1822 – 1911). Quetelét foi "quem primeiro percebeu que a Estatística deveria ser baseada na noção de probabilidade" (MEMÓRIA, 2004, p. 20), além de ser o responsável pela fundação da Statistical Society of London, em 1834, posteriormente denominada Royal Statistical Society, enquanto Galton, segundo Memória (2004), dentre suas notáveis contribuições, desenvolveu conceitos relacionados a regressão e correlação.

A partir de 1853, realizaram-se oito edições de congressos internacionais de Estatística. Entretanto, devido a falta de organização e ao posterior falecimento de Quetelét, em 1874, os encontros quase se extinguiram, retomados e, 1885, nove anos após a última edição. Neste ano, foi fundado o International Statistical Institute - ISI -, em Londres, o qual teve como membros fundadores a considerada "elite mundial dos estatísticos naquela época em particular" (SANTOS, 2016, p. 57), além de estruturar a organização de congressos, assim como criar coletivos especializados entre seus membros.

No que diz respeito às questões curriculares, o Inter-American Statistical Institute – IASI, fundado em 1940, tornou-se um elo entre os Estados Unidos e a América Latina com a finalidade de assegurar o ensino de Estatística em diferentes níveis de ensino. Fruto de uma iniciativa de membros do ISI, teve como função principal a aproximação com centros de pesquisa de países subdesenvolvidos no período da Guerra Fria e foi responsável por resoluções e parâmetros para a implementação e reformulação de cursos de Estatística.

Em 1989, o National Council of Teachers of Mathematics – NCTM publicou o Curriculum and Evaluation Standards for School Mathematics, que estabelecia parâmetros e recomendações para o ensino de Matemática, apontando direções e metas para a melhoria deste processo. Neste documento consta o eixo "Análise de Dados e Probabilidade" como um dos cinco eixos formadores. Tanto ele quanto seu sucessor, Principles and Standards for School Mathematics, foram de grande importância para o estabelecimento da Estatística enquanto conteúdo da Matemática na educação básica, sendo o NCTM o responsável por oficializar a "importância da abordagem dos conteúdos de Estatística no ensino básico, chamando atenção para as particularidades do seu ensino dentro dos conteúdos de Matemática em todo o mundo". (SANTOS, 2016, p. 59)

Outras alterações nas instituições relacionadas à Educação Estatística ocorreram, como a extinção do comitê de educação do ISI, em 1991 e deu lugar a International Association for Statistical Education – IASE, atual responsável pela organização do ICOTS, e a fusão do IASE com o International Study Group for Research on Learning Probability and Statistics, em 2000, constituindo o IASE Statistical Education Research Group.

Batanero (2001) indica que o surgimento de um movimento mundial, na década de 1970, reconheceu elementos necessários para o desenvolvimento de conceitos estatísticos, como a necessidade desenvolvimento do raciocínio probabilístico, de romper com o perfil determinístico nas aulas de Matemática e as dimensões éticas e políticas do uso da Estatística. Este foi o movimento que originou o que hoje se denomina Educação Estatística. O efeito percebido com esse movimento foi o ensino da Estatística no ensino básico, o que despertou reflexões sobre aspectos didáticos do ensino de Estatística, Probabilidade e Combinatória.

No Brasil, os reflexos desse movimento foram percebidos na publicação dos Parâmetros Curriculares Nacionais - PCN (BRASIL, 1997), que teve influência de diversas experiências de diferentes países, inclusive das trazidas pelo NCTM. Tendo o bloco de conteúdos "Tratamento da Informação" como responsável por englobar a "noções de estatística, de probabilidade e de combinatória" (BRASIL, 1997, p. 40), indicando procedimentos para o desenvolvimento de tais conceitos e reconhecimento de sua importância social.

Atualmente, a Base Nacional Comum Curricular (BRASIL, 2017) aborda, através de unidades temáticas, habilidades a serem desenvolvidas com os estudantes ao longo da Educação Básica. Aqui, a unidade temática "Probabilidade e estatística" relaciona os objetos de conhecimento às habilidades a serem desenvolvidas com os estudantes. Tal perspectiva vai de encontro com a ideia preconizada por pesquisadores da Educação Estatística, no que diz respeito ao desenvolvimento das competências estatísticas destacadas na sequência.

É recorrente a comparação quanto aos conceitos relacionados à Estatística aos relacionados à Matemática. Entretanto, devemos manter a distinção entre tais áreas, dado que, diferentemente do que é percebido na Matemática quanto ao seu caráter determinístico, a Estatística não o é. Moore (2004) nos afirma que, apesar das semelhanças, a Educação Matemática está para a Educação Estatística assim como a Matemática está para a Estatística: a segunda não é subárea da primeira e, se não as vemos assim, estaremos limitando a Estatística ao estudo da Probabilidade. Por isso, é necessário que analisemos aspectos relevantes à Educação Estatística que não se fazem necessárias à Educação Matemática.

Batanero (2001) observa que “é preciso experimentar e avaliar métodos de ensino adaptados à natureza específica da Estatística, pois a ela nem sempre se podem transferir os princípios gerais do ensino da Matemática” (p. 6).

Conforme Campos (2007), os conteúdos e valores desenvolvidos pela Estatística se diferenciam dos da Matemática, apesar de fazer uso de entes matemáticos atuando como coadjuvantes. Enquanto a Matemática, conforme já citado, tem caráter determinístico, a Estatística é permeada pelos princípios da aleatoriedade e da incerteza, por exemplo, que fogem ao escopo matemático. Além disso, a existência de elementos subjetivos, como a possibilidade de escolha da organização e apresentação dos dados, sua interpretação, reflexão, análise e tomada de decisões, que emergem como protagonistas dentre os objetivos da disciplina, distinguem o foco da Estatística em relação à Matemática. Nas palavras de Campos (2007), perceber essa diferenciação

[...]leva a uma tomada de consciência sobre os aspectos peculiares à Estatística, que se apresenta como uma ciência em franca evolução, que experimenta mudanças progressivas tanto do ponto de vista de seu conteúdo como de suas demandas de formação. (p. 48)

Nessa perspectiva, diversos autores divulgaram estudos que indicam que o planejamento da formação estatística de um sujeito deve seguir rumo ao desenvolvimento de três grandes competências, sem as quais não seria possível aprender conceitos estatísticos: letramento, raciocínio e pensamento estatísticos.

Diante disso, abordaremos cada uma dessas competências, detalhando as ideias propostas desses pesquisadores.

O termo letramento está diretamente relacionado a habilidade de ler, compreender, interpretar, analisar e avaliar elementos por meio de sua leitura. Quando este conceito é trazido para a Educação Estatística, temos diferentes leituras a seu respeito, entretanto elas convergem para a ideia de comunicação estatística, compreendendo, desta forma, a leitura, a escrita, a demonstração e troca de informações de diferentes elementos estatísticos (tabelas, gráficos, medidas-resumo), numa perspectiva crítica sobre tais informações

Gal (2002) define letramento estatístico como a habilidade de um indivíduo interpretar, avaliar criticamente e comunicar informações estatísticas. Além disso, em (GAL, 2004) há a ênfase de que tal competência se refere a dois componentes inter-relacionados:

1. habilidade de interpretar e avaliar criticamente as informações estatísticas, os argumentos relacionados com os dados de pesquisa e os fenômenos estocásticos que podem ser encontrados em diferentes contextos;
2. habilidade para discutir ou comunicar suas reações a essas informações estatísticas, tais como suas interpretações, suas opiniões e seus entendimentos sobre o seu significado.

Tais habilidades não devem ser vistas de forma isoladas, além de estarem correlacionadas com uma série de conhecimentos estatísticos e com atitudes que devem ser desenvolvidas e valorizadas nos estudantes. Nessa perspectiva, Campos, Wodewotzki e Jacobini (2013) nos dizem que além dos conhecimentos matemáticos e estatísticos, o estudante necessita ter entendimento do contexto do problema. Ainda assim, são necessários elementos adicionais para avaliação crítica da informação, como ter a atitude de fazer questionamentos, agindo ativamente sobre os dados e resultados obtidos.

Watson (1997) descreve o letramento estatístico como a capacidade de compreensão do texto e do significado das implicações das informações estatísticas inseridas em seu contexto formal e identifica três estágios de seu desenvolvimento:

1. o entendimento básico da terminologia estatística;
2. o entendimento da linguagem estatística e os conceitos inseridos num contexto de discussão social;
3. o desenvolvimento de atitudes de questionamento nas quais se aplicam conceitos mais sofisticados para contradizer alegações que são feitas sem fundamentação estatística apropriada.

Garfield e Gal (1999) explicam que o uso da linguagem estatística, isto é, terminologia, símbolos e termos, a habilidade de interpretar gráficos e tabelas e compreender informações estatísticas em diferentes mídias são destaque do letramento estatístico.

Rumsey (2002) expõe que:

Primeiro, nós queremos que nossos alunos se tornem bons ‘cidadãos estatísticos’, entendendo estatística o suficiente para ser capaz de consumir as informações com as quais somos inundados diariamente, pensando criticamente sobre essas informações e tomando boas decisões com base nelas. Alguns pesquisadores chamam isso de letramento estatístico (p.1).

Snee (1999) nos indica que a pesquisa, a prática e a educação estatística entraram em uma nova era, na qual, o foco estava no desenvolvimento do pensamento estatístico. Isso só foi possível graças ao desenvolvimento de recursos tecnológicos que possibilitaram aos estudantes que os cálculos permanecessem em segundo plano, dando espaço para a compreensão dos processos e interpretação dos resultados (CAMPOS, 2007).

Três questionamentos básicos são apontados por Chance (2002) sobre o pensamento estatístico:

1. O que é pensamento estatístico?
2. Como podemos ensinar o pensamento estatístico?
3. Como podemos determinar se os estudantes estão pensando estatisticamente?

Mallows (1998) apresenta a ideia de que o pensamento estatístico corresponde a capacidade de relacionar dados estatísticos com situações reais, tendo em mente a existência da incerteza e da variabilidade, buscando novos conhecimentos a partir dos dados conhecidos. Assim, o pensamento estatístico ocorre quando se associa um modelo matemático à natureza do problema em questão, isto é, se identifica a situação analisada e há a escolha adequada do ferramental estatístico que possibilite sua descrição e interpretação. De encontro a essa noção, Campos (2007) afirma que:

O entendimento dos padrões e estratégias de pensamento usados pelos estatísticos e suas integrações para solucionar problemas reais é fundamental para desenvolver o pensamento estatístico nos estudantes. (p.53)

Conforme Chance (2002), o pensador estatístico é capaz de questionar espontaneamente e investigar os resultados relacionados aos dados de um certo contexto, indo além daquilo que, de fato, trabalha-se nas aulas de estatística. Com isso, é possível concluir que, dentre as características do pensamento estatístico, encontra-se o desenvolvimento da habilidade de visualizar o processo estatístico de maneira global, identificando e analisando as interações existentes no dado contexto e os motivos destes, assim como compreender suas relações e o significado de possíveis variações, extrapolar a interpretação dos dados naquilo que é prescrito nos textos e propor questões e pressuposições não previstas inicialmente.

Tendo em vista tais componentes do pensamento estatístico, o desafio passa a ser o desenvolvimento destes junto aos estudantes. Nessa perspectiva, Campos, Wodewotzki e Jacobini (2013) explicam que:

Apesar de não ser possível ensiná-los diretamente aos alunos, acreditamos na viabilidade de trabalhar na valorização dos hábitos mentais que permitem aos não estatísticos apreciar melhor o papel e a relevância desse tipo de pensamento, provendo experiências que valorizem e reforcem os tipos de estratégias que desejamos que eles empreguem no tratamento de novos problemas. (p. 39)

Desta forma, é necessária uma proposta de trabalho que se proponha a desenvolver alguns hábitos mentais e habilidades de resolução de problemas necessários para o pensamento estatístico. Nessa perspectiva, Chance (2002) destaca como essenciais:

1. a consideração sobre como melhor obter dados significantes e relevantes para responder à questão que se tem em mãos;
2. a reflexão constante sobre as variáveis envolvidas e a curiosidade por outras maneiras de examinar os dados e o problema que se tem em mãos;
3. a visão do processo por completo, com constante revisão de cada componente;
4. o ceticismo onipresente sobre a obtenção dos dados;
5. o relacionamento constante entre os dados e o contexto do problema e a interpretação das conclusões em termos não estatísticos;
6. a preocupação com o pensar além do livro-texto.

Campos (2007) contribui com a discussão, ao complementar acerca da necessidade de que os dados a serem trabalhados pelos estudantes possuam algum significado, além de se evitar atividades que envolvam apenas cálculos ou reprodução de algoritmos relacionados ao tratamento de dados de forma estritamente numéricos, de tal modo que se conheça a finalidade do uso dos dados específicos e em que contexto foram coletados.

Os estudantes, além de desenvolverem os hábitos mentais e habilidades citadas, devem acreditar nas técnicas que se utilizam para o tratamento de dados (CAMPOS, 2007). Campos, Wodewotzki e Jacobini (2013) ainda complementam, ao afirmar que

Para que exista essa crença, é necessário que eles saibam por que estão usando esta ou aquela técnica, ou ainda, como o uso de uma técnica diferente influenciaria os resultados de uma pesquisa. (p. 40)

Outro ponto a ser considerado, segundo Hoerl (1997), está relacionado ao uso completo dos processos de pesquisa estatística, visto que, segundo o autor, o entendimento e a retenção dos conteúdos estatísticos podem ser ampliados. De encontro a essa ideia, Campos, Wodewotzki e Jacobini (2013) explanam acerca da relevância dos dados e da pesquisa realizada serem constantemente questionados pelos estudantes. Desta forma, percebe-se o pensamento estatístico como uma competência além das habilidades de uso de ferramentas de cálculo inerentes ao contexto estatístico, mas sim, a percepção, compreensão e crítica do processo.

Pfannkuch e Wild (2004) propuseram cinco tipos de pensamentos considerados fundamentais, sendo eles:

1. Reconhecimento da necessidade de dados: está relacionado com os fundamentos da investigação estatística, os quais baseiam-se no pressuposto de que muitas situações reais não podem ser julgadas sem a coleta e análise de dados coletados adequadamente. A evidência anedótica ou a própria experiência pode não ser confiável e enganosa para julgamentos e tomada de decisões. Portanto, dados coletados adequadamente são considerados um requisito primordial para julgamentos confiáveis sobre situações reais.
2. Transnumeração: trata sobre a mudança de registros de representação de modo a possibilitar a compreensão do problema. Tal tipo de pensamento ocorre quando (i) são encontradas medidas de caracterizam ou designam qualidades de uma situação real; (ii) são gerados gráficos e tabelas a partir dos dados coletados; e (iii) o significado dos dados e o julgamento sobre tais são comunicados de forma que sejam compreendidos pelos receptores.
3. Consideração sobre a variação: se baseia em perceber como as estratégias utilizadas para estudar os dados sofrem influência da variação desses. Inclui-se, aqui, as tomadas de decisão relacionadas a redução da variabilidade, como, por exemplo, ignorar ou não outliers, corrigir erros de medidas, entre outros;
4. Raciocínio com modelos estatísticos: trata-se de um pensamento sobre o comportamento global dos dados. Pode ser acessado por meio de uma análise de regressão, séries temporais, ou por meio de ferramentas muito mais simples, como gráficos estatísticos ou medidas de tendência central;
5. Integração contextual da Estatística: corresponde a análise dos resultados dentro do contexto do problema estudado e da validação destes de acordo com os conhecimentos relacionados a esse contexto.

É importante percebermos a necessidade de uma mudança de paradigma para que o estudante seja capaz de desenvolver tais pensamentos. Com isso, é necessário um processo de revolução interna com o intuito de abrir mão do olhar determinístico sobre o mundo, inerente ao ambiente matemático, para adoção de uma visão probabilística, levando em consideração a variabilidade e o processo estatístico envolvido na pesquisa realizada.

Em síntese, podemos entender que ao desenvolver o pensamento estatístico estamos em busca da compreensão dos modelos de problemas e quais ferramentas de resolução cada modelo descreve, com a meta de reconhecer a aplicabilidade dessas ideias nos problemas reais. Para tanto, é necessário que as questões inerentes ao processo de ensino e aprendizagem envolvidas num trabalho quantitativo superem o estudo de métodos e conceitos estatísticos, assim como se desenvolvam num contexto significativo para os estudantes, por meio do uso de dados reais, principalmente, coletados pelos próprios estudantes.

Garfield (2002) define o raciocínio estatístico como a maneira com a qual uma pessoa raciocina com ideias estatísticas e dá sentido às informações estatísticas. Isso envolve fazer interpretações sobre dados, representações gráficas, construção de tabelas etc. Frequentemente, o raciocínio estatístico relaciona as ideias de amostragem, aleatoriedade, chance, probabilidade, incerteza, variabilidade, distribuição, testes de hipóteses, o que leva a interpretações e inferências acerca dos resultados.

Com o objetivo de diferenciar o raciocínio estatístico do Raciocínio matemático, Moore (1992) nos expõe que “A Estatística tem sua própria substância, seus próprios conceitos e modos de raciocínio. Esses devem ser o coração do ensino de Estatística para os iniciantes em qualquer nível” (p. 14).

Gal e Garfield (1997) fazem, também, uma distinção entre a Estatística e a Matemática, no que diz respeito ao raciocínio, tomando como premissas as seguintes ideias:

1. Na Estatística, os dados são visualizados como números inseridos num dado contexto, no qual atuam como base para a interpretação de resultados.
2. Os conceitos e procedimentos matemáticos são usados como parte da solução de problemas estatísticos. Porém, a necessidade de buscar resultados mais expressivos ou precisos nos levou a, cada vez mais, fazer uso de recursos tecnológicos, principalmente computadores e softwares, que se encarregam de fazer a parte operacional.
3. A natureza fundamental de muitos problemas estatísticos é a de que eles comumente não têm uma única solução matemática. Os problemas de Estatística geralmente começam com um questionamento e terminam com uma opinião, que se espera que seja fundamentada em certos resultados teórico-práticos. Os julgamentos e as conjecturas expressos pelos estudantes frequentemente não podem ser caracterizados como certos ou errados. Em vez disso, eles são analisados quanto à qualidade de seu raciocínio, adequação e métodos empregados para fundamentar as evidências.

Garfield e Gal (1999, pp. 12-13) estabelecem alguns tipos específicos de raciocínio que são desejáveis que os estudantes, no contexto do Ensino Superior, desenvolvam enquanto aprendem Estatística:

1. Raciocínio sobre dados: reconhecer e categorizar os dados (qualitativos, quantitativos discretos ou contínuos), entender como cada tipo de variável leva a um tipo particular de tabela, gráfico ou medida estatística.
2. Raciocínio sobre representação dos dados: entender como ler e interpretar gráficos, como cada tipo de gráfico é apropriado para representar um conjunto de dados, reconhecer as características gerais de uma distribuição pelo gráfico, observando a forma, o centro e o espalhamento.
3. Raciocínio sobre medidas estatísticas: entender o que as medidas de posição e variabilidade dizem a respeito do conjunto de dados, quais são as medidas mais apropriadas em cada caso e como elas representam o conjunto de dados. Usar as medidas de posição central e de variabilidade para comparar diferentes distribuições e entender que amostras grandes são melhores do que as pequenas para se fazer previsões.
4. Raciocínio sobre incerteza: entender e usar as ideias de chance, aleatoriedade, probabilidade e semelhança para fazer julgamentos sobre eventos, usar métodos apropriados para determinar a semelhança de diferentes eventos (como simulações com moedas ou diagramas de árvore, que ajudam a interpretar diferentes situações).
5. Raciocínio sobre amostras: entender como as amostras se relacionam com a população e o que pode ser inferido acerca de uma amostra, saber que amostras grandes e bem selecionadas representarão melhor a população. Tomar precauções quando examinar a população com base em pequenas amostras.
6. Raciocínio sobre associações: saber julgar e interpretar as relações entre variáveis, em tabelas de dupla entrada ou em gráficos, entender que uma forte correlação entre duas variáveis não significa que uma causa a outra.
7. Os conceitos e procedimentos matemáticos são usados como parte da solução de problemas estatísticos. Porém, a necessidade de buscar resultados mais expressivos ou precisos nos levou a, cada vez mais, fazer uso de recursos tecnológicos, principalmente computadores e softwares, que se encarregam de fazer a parte operacional.
8. A natureza fundamental de muitos problemas estatísticos é a de que eles comumente não têm uma única solução matemática. Os problemas de Estatística geralmente começam com um questionamento e terminam com uma opinião, que se espera que seja fundamentada em certos resultados teórico-práticos. Os julgamentos e as conjecturas expressos pelos estudantes frequentemente não podem ser caracterizados como certos ou errados. Em vez disso, eles são analisados quanto à qualidade de seu raciocínio, adequação e métodos empregados para fundamentar as evidências.

Apesar das ideias desenvolvidas acerca do raciocínio estatístico, não há consenso entre os pesquisadores no que diz respeito ao seu desenvolvimento junto aos estudantes. Muitos autores afirmam não ser possível fazê-lo por instrução direta, e muitos notam pouco ou nenhum avanço mesmo seguindo as recomendações descritas. Sedlmeier (1999) afirma que raramente o raciocínio estatístico é ensinado e, quando há uma tentativa, ela é mal sucedida. Em contraponto, Nisbett (1993) expõe que, se o estudante aprender as regras estatísticas e estas forem ensinadas por instrução direta, o raciocínio estatístico de tais estudantes pode ser aprimorado. Entretanto, Garfield (1998) sugere que, ao invés dos professores ensinarem a usar e aplicar o raciocínio estatístico, eles ensinam conceitos e procedimentos, com o uso de dados reais, além do apoio de softwares, de modo ao raciocínio estatístico ser fruto dessa experiência. Mas Garfield (2002), aparentemente, resgata a ideia de modo a trazer a dúvida ao debate, quando afirma que:

Não há um consenso entre os pesquisadores sobre como ajudar os estudantes a desenvolver o raciocínio estatístico ou como determinar o correto nível de seu raciocínio. Talvez com mais estudos em sala de aula que examinem os tipos de raciocínio, os conhecimentos de pré-requisito e as habilidades necessárias a cada tipo de raciocínio, além do impacto de diferentes atividades de ensino, os pesquisadores possam ser capazes de entender o processo de como se desenvolve corretamente o raciocínio estatístico (p. 4).

Por fim, Garfield (2002) apresenta cinco níveis de raciocínio estatístico:

• Nível 1 – Raciocínio idiossincrático. O estudante sabe algumas palavras e símbolos estatísticos, usa-os mesmo sem entendê-los completamente e mistura-os com informações não relacionadas. Por exemplo: os estudantes aprenderam os termos média, mediana e moda como medidas de resumo, mas fazem uso incorreto delas (por exemplo, comparando a média com mediana).
• Nível 2 – Raciocínio verbal. O estudante tem entendimento verbal de certos conceitos, mas não aplica isso em seu comportamento. Por exemplo, o estudante pode selecionar ou prover uma correta definição, mas não entende completamente o seu conceito (por exemplo, porque a média é menor que a mediana em distribuições com assimetria negativa).
• Nível 3 – Raciocínio transicional. O estudante é capaz de identificar corretamente uma ou duas dimensões de um processo estatístico, mas sem integrar completamente essas dimensões. Por exemplo, uma amostra maior leva a um intervalo de confiança menor, um desvio padrão menor leva a um intervalo de confiança menor.
• Nível 4 – Raciocínio processivo. O estudante é capaz de identificar corretamente as dimensões de um conceito ou processo estatístico, mas não integra completamente essas dimensões ou não entende o processo por completo. Por exemplo, o estudante sabe que a forte correlação entre duas variáveis não implica necessariamente que uma causa a outra, mas não pode explicar o porquê.
• Nível 5 – Raciocínio processual integrado. O estudante tem um completo entendimento sobre um processo estatístico, coordenando as regras e o comportamento da variável. O estudante pode explicar o processo com suas próprias palavras e com confiança. Por exemplo, o estudante pode explicar o que um intervalo de confiança de 95% significa em termos do processo se obtiver uma distribuição amostral de uma população.

Este tópico tem por objetivo apresentar um breve histórico acerca da transposição da Modelagem Matemática vinculada à área de Matemática Aplicada para o contexto educacional, com enfoque na produção nacional. Na sequência, exploraremos as perspectivas de trabalho em Modelagem na Educação Matemática, propostas por Kaiser e Sriraman (2006), de modo a compreender como diferentes pesquisadores abordam tal metodologia. Por fim, realizaremos uma discussão pontual sobre a perspectiva sócio-crítica de Modelagem na Educação Matemática (BARBOSA, 2001) e seu entrelaçamento com o movimento da Educação Matemática Crítica (SKOVSMOSE, 2001).

A palavra modelo nos remete a ideia de representação. De forma geral, podemos criar modelos com a finalidade de interpretar e compreender fenômenos, sejam eles naturais ou sociais. Alguns exemplos famosos são o modelo de crescimento populacional malthusiano e o decaimento radioativo, que auxiliam a ciência a descrever tais eventos. Tais modelos são responsáveis pelo desenvolvimento de diversos conhecimentos científicos já superados, muitos com apoio das tecnologias atuais que propiciam a replicação virtual de um experimento por uma enorme quantidade de repetições, ou ainda vigentes, o que explica a importância desses no desenvolvimento científico.

Nessa perspectiva, um conjunto de símbolos e relações matemáticas que procura traduzir, de alguma forma, um fenômeno em questão ou problema de situação real, denomina-se ‘modelo matemático’ (BIEMBENGUT; HEIN, 2003, p.12).

O processo que envolve a criação de um modelo matemático é conhecido como modelagem matemática, que, conforme Biembengut e Hein (2003), é

uma arte, ao formular e elaborar expressões que valham não apenas para uma solução particular, mas que também sirvam, posteriormente, como suporte para outras aplicações e teorias

Já Almeida e Ferruzzi (2009) expõem que o termo "modelagem matemática" remete "à busca de uma representação matemática para um objeto ou um fenômeno que pode ser matemático ou não" (p. 120).

Conforme Caldeira, Silveira e Magnus (2011), no Brasil, a Modelagem na Educação Matemática surgiu como uma possibilidade de ensino e aprendizagem de Matemática na década de 1970. Silveira (2007) afirma que, em 1976, Celso Braga Wilmer defendeu a primeira dissertação sobre o tema, sob orientação de Aristides Camargo Barreto, na Universidade Católica do Rio de Janeiro. À época, cunhou-se o termo "modelos na aprendizagem matemática". Desde então, até o ano de 2005, em sua pesquisa acerca da Modelagem Matemática em Educação no Brasil, Silveira (2007) contabilizou 65 dissertações e teses sobre o tema.

Biembengut (2012) corrobora tal proposição, ao indicar que a Modelagem Matemática "[...] na Educação Básica e Superior passa a ocorrer a partir da década de 1970, praticamente ao mesmo tempo em diversos países, inclusive no Brasil" (p. 196). A autora ainda informa que o movimento iniciou com professores do Ensino Superior, particularmente com aqueles que atuavam nos cursos de Engenharia como tentativa de responder ao questionamento frequente dos alunos: "para que serve a matemática?". Alguns dos precursores também são citados.

[...] Aristides Camargo Barreto, do Brasil, que fez uso dos processos da modelagem em suas aulas de Cálculo Diferencial Integral e Análise Matemática em Cursos de Engenharia e de Matemática nos anos de 1970 e 1980; e David Burghes, do Reino Unido, que, além da graduação, passou a desenvolver projetos com professores do Ensino Médio para produzir materiais de modelagem. (BIEMBENGUT, 2012, p. 196)

Acerca do desenvolvimento da Modelagem na Educação Matemática no Brasil, Biembengut (2009) propõe sua organização em três fases. A Primeira Fase (1976-1986) se alicerça nas três primeiras produções a nível de pós-graduação, duas com temática relacionada ao uso de modelos matemáticos no ensino, defendendo seu uso, porém sem explicitar quais modelos utilizar ou como construir um modelo, e outra relacionando apenas teoricamente modelos matemáticos e modelos de aprendizagem. Já a Segunda Fase, é marcada por sete produções desenvolvidas na Universidade Estadual Paulista (UNESP) de Rio Claro, que possui um dos primeiros Programas de Pós-Graduação de Educação Matemática do Brasil. Tais produções se propõe a validar ou analisar a modelagem matemática na Educação em diferentes níveis e modalidades de ensino. Além disso, emerge a concepção de Rodney Bassanezi, assim como conceitos e definições sobre modelagem no ensino em publicações internacionais, além da consolidação do Grupo Internacional de Modelagem e Aplicações Matemáticas (International Community of Teachers of Mathematical Modelling and Applications - ICTMA), em 1986. Por fim, a Terceira Fase corresponde ao período a partir de 1991, que converge a um período de ampliação da produção acerca da Modelagem Matemática no Ensino (SILVEIRA, 2007, pp. 21-23), no qual, além dos precursores do movimento, seus orientados começam a desenvolver pesquisas acerca da temática, expandindo a produção a outros programas de pós-graduação pelo Brasil, com grande parte de seu referencial teórico alicerçado por pesquisadores brasileiros.

Das possibilidades metodológicas possíveis para a efetivação do trabalho de Educação Estatística, Campos, Wodewotzki e Jacobini (2013) apontam como possibilidade o uso da pedagogia de projetos, dada a natureza desta proposta, na qual tem a “explícita intenção de transformar o aluno de objeto em sujeito” (p. 46). Nesta proposta, percebe-se que na Educação Matemática brasileira é vinculado, em muitas situações, à aplicação da Modelagem Matemática. Na perspectiva da Modelagem Matemática como metodologia de ensino, Barbosa (2001) define que “Modelagem é um ambiente de aprendizagem no qual os estudantes são convidados a indagar e/ou investigar, por meio da Matemática, situações oriundas de outras áreas da realidade” (p. 6).

Por algum tempo, o foco da Educação Matemática encontrava-se nos conteúdos e do ensino e aprendizagem destes. Entretanto, a partir da década de 1980, pensadores de diferentes partes do mundo buscaram criticar a aprendizagem matemática e a sua função na sociedade, em diversos aspectos como econômicos, culturais, sociais, entre outros. Inspirada na Teoria Crítica da Sociedade, a Educação Crítica propõe-se a contrapor o “tradicionalismo no sistema educacional” (CAMPOS et al, 2011) e foi constituída a partir da revisão da tradição filosófica e política Ocidental realizada por Jurgen Habermas, na Alemanha, e pela prática social em organismos sociais, na promoção de uma educação para a consciência crítica de Paulo Freire, no Brasil, dois pensadores do Século XX. Freire contribuiu não só através de sua prática, mas com os ensaios teóricos e a carreira acadêmica, realizando críticas à desigualdade social gerada pelo modelo capitalista, moldando a Educação Crítica em uma vertente de democracia plena.

Da perspectiva freireana, Skovsmose (2001) desenvolve o pensamento da Educação Matemática Crítica, a qual defende a Educação Crítica indissociada da realidade social, da desigualdade e dos demais problemas decorrentes desta realidade. Desta forma, o processo educacional deve estar vinculado à comunidade escolar e a realidade do aluno.

Ainda sobre o panorama atual do Ensino de Matemática, podemos situar a resolução de problemas fechados como uma das possibilidades de trabalho mais frequentes (COTTON, 1998 apud SKOVSMOSE, 2000; FIORENTINI, 2011). Assim, a proposta utilizada versa sobre a exposição de conceitos e técnicas matemáticas e, posteriormente, o desenvolvimento de atividades fechadas em busca da única resposta correta. Esta estratégia, denominada paradigma do exercício (SKOVSMOSE, 2000), baseia-se no treinamento do indivíduo quanto ao uso da Matemática de forma isolada e dando o sentido de seu ensino numa perspectiva dicotômica, do certo ou errado.

Ao invertermos a forma de compreendermos as relações que propiciam a construção de habilidades através do uso de raciocínio matemático, Skovsmose (2000) nos apresenta os cenários para investigação, que consiste num ambiente em que os alunos são convidados a realizar questionamentos e buscarem explicações para estes. Explicita-se nesta proposta o protagonismo do aluno no processo de investigação, enquanto o professor surge no papel de mediador deste processo.

Ao tratarmos do Ensino de Matemática, é possível evidenciar referências à produção de significados para conceitos matemáticos. Conforme Skovsmose (2000), as referências possíveis são à matemática pura - auto-referência - , à semi-realidade - realidade criada - e às situações da realidade. Os cenários de investigação, percebidos num contraponto ao paradigma do exercício e combinados às referências, convergem nos ambientes de aprendizagem, propostos por Skovsmose (2000), numa forma de organizar as diferentes práticas de ensino, possibilitando a classificação do ambiente criado na sala de aula. Desta combinação, obtém-se uma matriz com seis tipos diferentes de ambientes de aprendizagem (Quadro 1).

Quadro 1 - Ambientes de aprendizagem

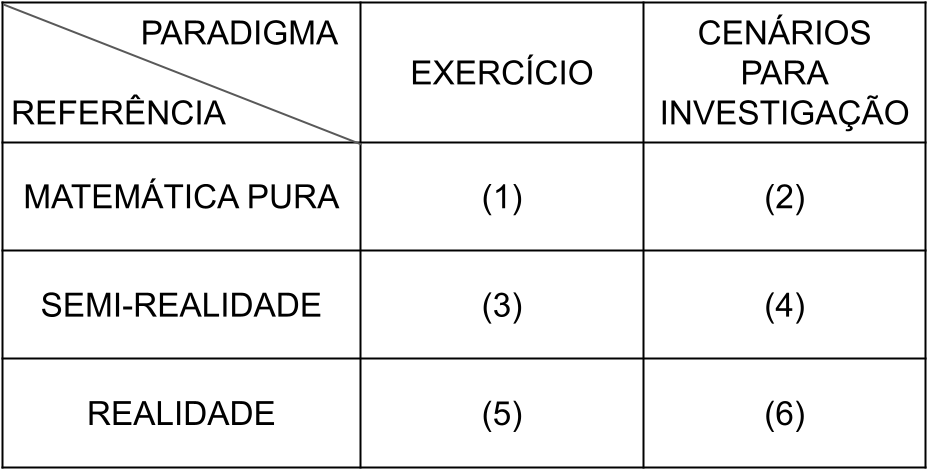
Fonte: SKOWSMOSE, 2000, p.8

Como fruto de uma sistematização de diferentes perspectivas de trabalho relacionadas à Modelagem na Educação Matemática, Kaiser e Sriraman (2006) categorizaram cinco perspectivas de trabalho desenvolvidas a nível mundial, assim como seus objetivos. São elas:

1. Perspectiva Realística ou Aplicada: Aprtesenta objetivos utilitários pragmáticos, ou seja, resolver problemas do mundo real, originários da indústria ou da ciência, entendê-los e solucioná-los com foco na promoção das competências de modelagem;
2. Perspectiva Contextual: Apresenta objetivos relacionados ao uso de problemas reais como promotores de motivação aos estudantes e baseia-se na interpretação do enunciado proposto, sendo a obtenção do modelo matemático uma tarefa de resolução de problemas, a partir da identificação de semelhanças a situações já solucionadas.
3. Perspectiva Educacional: Apresenta objetivos pedagógicos e relacionados ao tema de estudo, com enfoque na estruturação dos processos de aprendizagem e sua promoção através da Modelagem Matemática (Modelagem Didática), assim como da introdução e desenvolvimento de conceitos (Modelagem Conceitual);
4. Perspectiva Epistemológica ou Teórica: Apresenta como objetivo o desenvolvimento da teoria matemática;
5. Perspectiva Sócio-Crítica: Apresenta objetivos pedagógicos relacionados ao desenvolvimento do pensamento crítico sobre o papel e a natureza dos modelos matemáticos, além da função da matemática na sociedade. Relaciona-se com a ideia de formar estudantes autônomos e preparados para desempenhar a cidadania, a partir da reflexão acerca do contexto em que estes sujeitos estão inseridos.

As práticas pedagógicas apresentadas a seguir foram selecionadas por meio de uma revisão sistemática, considerando o período de publicação entre os anos de 2013 e 2018, no formato de artigos ou relatos de experiência, considerando o contexto dos Anos Finais do Ensino Fundamental. Para tanto, estabeleceu-se um conjunto de palavras-chaves que foram posteriormente combinadas, de modo a estabelecer as chaves de busca para trabalhos em Língua Portuguesa e Língua Inglesa. São elas: (1) Modelagem; (2) Educação Matemática; (3) Educação Estatística; (4) Ensino; (5) Aprendizagem; (6) Matemática; (7) Estatística.

De modo a delinear a busca pelos trabalhos, estabeleceu-se o conjunto de bases de conhecimento formados pelos sites Web of Science (WOS), CIEM, Periódicos CAPES, SCOPUS, SPRINGER, Journal of Urban Mathematics Education, Caminhos da Educação Matemática em Revista, International Journal for Research in Mathematics Education, Revista de Matemática, Ensino e Cultura, Revista Internacional de Pesquisa em Educação Matemática e Simpósio Internacional de Pesquisa em Educação Matemática. O levantamento de trabalhos foi realizado entre julho e setembro de 2018.

Da busca inicialmente realizada, resultaram 569 trabalhos, sendo selecionados 353 manuscritos, após análise dos resumos. Considerando critérios de inclusão e exclusão e a interseção entre as temáticas de Modelagem Matemática e Educação Estatística, reduziram-se a 5 publicações, as quais, apresentamos um breve relato.

Tendo como público-alvo estudantes do 7º ano do Ensino Fundamental de uma escola municipal de Sapucaia do Sul (RS), os pesquisadores, sendo a primeira, exercendo o papel de educadora-pesquisadora, organizaram uma turma em grupos contendo entre três e cinco componentes, com formação por livre iniciativa dos estudantes. Para tal experiência, os autores consideraram a ideia de Barbosa (2001), a qual Modelagem Matemática corresponde a um Ambiente de Aprendizagem em que os estudantes são convidados a questionar e/ou investigar, com auxílio da matemática, situações provindas de um contexto real.

No primeiro encontro, a educadora-pesquisadora introduziu a ideia de Estatística, suas finalidades, sua aparição no cotidiano, as fases do método estatístico e papel da Estatística na sociedade. Já no segundo encontro, os estudantes realizaram uma pesquisa na turma sobre um tema de interesse, tendo como objetivo a aplicação das ideias discutidas no encontro anterior, como as que emergiram na experiência (tabelas de frequência e gráficos).

O terceiro encontro foi conduzido através de uma atividade proposta pela educadora-pesquisadora e resolução orientada desta, tendo como temática o desempenho do Brasil nas Olimpíadas A partir dos dados disponíveis em jornais, os estudantes utilizaram gráficos de linhas e de colunas para representá-los. No quarto encontro se estabeleceram diferentes ambientes de aprendizagem, ora como cenário para investigação, ora como paradigma do exercício. Nesse, foi explorada a construção de gráficos de setores a partir do dado "número de reprovações" de cada estudante presente. Desta forma, além das noções estatísticas relacionadas a porcentagem e do processo de construção dos gráficos de setores, abordou-se as noções de proporcionalidade e equação (aspectos algébricos), assim como a medida de ângulos (aspecto geométrico).

Os autores constataram que a experiência propiciada contribuiu para a criação de Ambientes de Aprendizagem nos quais os estudantes foram capazes de desenvolver autonomia e pensamento crítico. Também citam que os conteúdos emergentes da experiência tiveram significados diferentes do que quando trabalhados individualmente e descontextualizados. Apesar de não se deterem às análises das competências estatísticas, os pesquisadores concluíram que se torna válida a introdução de conteúdos relacionados à Estatística em um Ambiente de Aprendizagem construído por meio da Modelagem Matemática.

Com o objetivo de propiciar aos alunos que se apropriassem de conceitos estatísticos a partir de um estudo sobre os óbitos dos escravos do Rio Grande do Sul no Séc. XIX, as pesquisadoras construíram uma proposta em que a educadora-pesquisadora (primeira autora do artigo) propôs um tema de pesquisa no qual o aluno foi convidado a buscar informações, se posicionar e defender seus argumentos, realizando cálculos matemáticos, construindo tabelas e gráficos para com suas próprias análises responder à problematização do tema proposto.

O interesse no tema da escravidão no Séc. XIX no RS, inicia a partir da necessidade de se debruçar um pouco mais em questões centrais que caracterizaram esse período, a saber às condições de vida da época e a respeito da morte dos escravos. Entre outras contribuições, essa pesquisa pôde auxiliar no entendimento de doenças e epidemias da época, além de assuntos relacionados com etnias, escravidão e preconceitos, visando instigar e preparar o aluno para o exercício da cidadania crítica, reflexiva e participativa.

Alunos do sétimo ano foram convidados a fazer uma experiência de pesquisa de iniciação científica, orientada pelos seus professores de Matemática, Geografia, História e Ciências. Tendo como base um projeto totalmente multidisciplinar, se constituiu um grupo de 9 alunos voluntários para participar do projeto, com idades entre 12 e 13 anos, sendo 6 meninas e 3 meninos.

Para iniciar essa experiência, os alunos e educadora-pesquisadora trouxeram para a sala de aula diferentes conceitos acerca da população e amostra. Foram utilizados os registros contidos no livro “Africanos na Santa Casa de Porto Alegre: óbitos dos escravos sepultados no cemitérios da Santa Casa (1850-1855)”, obra de Flores (2007). Ficou definido que a população a ser analisada seria os escravos sepultados no Cemitério Santa Casa, entre os anos de 1850 e 1855.

Na etapa seguinte, um formulário do google docs foi elaborado e preenchido com os dados de uma amostra aleatória de 1559 casos de óbitos, de um total de aproximadamente 7000 registros do livro. Desta forma, se criou um banco de dados e por meio de dele foi possível gerar gráficos e tabelas. Na sequência, elegeram-se as variáveis de estudo, que foram: etnias, escravidão, preconceito, doenças e epidemias de época, buscando relações com a causa da morte dos cativos.

As atividades foram realizadas em 14 encontros no primeiro semestre de 2016. Os alunos foram convidados a pensar nas diferentes causas de morte dos escravos e associá-las com as possíveis condições de vida. Posteriormente, visitaram o Arquivo Histórico Santa Casa de Misericórdia onde os alunos puderam conhecer um pouco mais sobre a história do Complexo Hospitalar de Misericórdia Santa Casa, com ênfase ao seu caráter de assistência e manusear o livro de óbitos original.

Conforme as autoras, foi possível observar o interesse e envolvimento da turma, em relação a temática abordada, mas, sobretudo, da possibilidade de por meio da estatística estudar e interrelacionar diferentes disciplinas. A facilidade no entendimento e na escolha da amostra surpreendeu a educadora-pesquisadora.

Partiu do grupo de alunos a ideia de selecionar a cada quatro colunas de registro do livro, uma delas, de maneira aleatória para compor a amostra. Ou seja, os alunos demonstraram entendimento a respeito de que uma amostra deve ser representativa e aleatória.

Uma das tarefas designadas aos alunos foi que explorassem o tutorial do Google Forms para criar um formulário online. Não se observou nenhum tipo de dificuldade ou obstáculo nessa etapa.

A tarefa seguinte foi responder o Formulário Google para a formação de nosso banco de dados. As questões respondidas foram: nome, etnia, nacionalidade, estado civil, idade de falecimento, ano do falecimento e a causa mortis.

Após o término da digitação, houve a leitura crítica do banco de dados, em busca de erros de digitação. Os erros encontrados foram corrigidos, e na impossibilidade de correção, o questionário seria excluído. Ficou-se com 1599 registros validados, com os quais, por meio do uso da função “filtro” da Planilha do Excel, os alunos criaram diferentes tabelas e gráficos. Os mesmos também foram fontes de estudo para as demais disciplinas desse trabalho.

O grupo percebeu alguns problemas enquanto respondiam o questionário, a falta de informação da idade dos escravos e o entendimento da nacionalidade. Ficou estabelecido que fosse acrescentada a palavra meses para os menores de um ano de idade. Também foi decidido escrever “não informado” na falta de registro. Quanto à nacionalidade, o professor de História observou que há duas: escravo crioulo e africano.

Os alunos desenvolveram conhecimentos sobre a construção de distribuições de frequência e de gráficos adequados, que foram usados junto com textos descritivos e interpretativos para compor o relatório escrito que sintetizasse os principais assuntos abordados pelas disciplinas afins. Nesse eixo, merece destaque o uso de tecnologias, como o uso do Google Forms e também o uso de planilhas eletrônicas, que ajudam na construção de gráficos, para avaliar e comparar resultados.

Os alunos se envolveram no entendimento da morte dos escravos, que remete às suas condições de vida, sugerindo mudanças com base em suas reflexões sobre as questões abordadas nas aulas. Tais questões permeavam entre a aplicabilidade e a utilidade, a investigação e a pesquisa, a reflexão e a crítica, o que permitiu que eles analisassem como a matemática pode ser usada nas práticas sociais, através da Estatística, como instrumento desencadeador de um trabalho interdisciplinar.

Através dos estudos de Estatística, foi possível perceber as condições precárias que se encontravam os escravos no íntegro da população: viviam em lugares baixos, mal arejados, poucos espaçosos e aglomerados.

A Modelagem Matemática possibilitou aos alunos a oportunidade de vivenciar aulas com um envolvimento e colaboração de todos, na realização de um trabalho investigativo. Os alunos conseguiram perceber a aplicabilidade dos saberes acadêmicos, pois conectaram mais de um componente escolar na validação das soluções por eles encontradas.

Pode-se afirmar que as atividades proporcionaram momentos de cooperação entre os alunos, com envolvimento e comprometimento nas aprendizagens vivenciadas, despertando a motivação pelo estudo de conceitos de Estatística e desenvolvendo a competência para planejar e construir relatórios de pesquisas estatísticas descritivas, diferenciando pesquisa populacional de pesquisa amostral.

Assim, através da Estatística, os alunos refletiram criticamente sobre as questões que envolvem os escravos para responder a seus questionamentos nos aspectos socioculturais, ambientais, oriundos de outras disciplinas escolares, em especial a História e Ciências.

Com o objetivo de mostrar que o ensino-aprendizagem através da Modelagem Matemática pode ser aplicada em sala de aula, a fim de despertar no aluno o interesse pela disciplina que é vista pela maioria como desconectada do cotidiano, se construiu um ambiente pedagógico que o aluno pudessem vivenciar a aplicabilidade dos conteúdos estatísticos, ao mesmo tempo em que desenvolviam a capacidade de pesquisar, de realizar trabalhos em grupo, de discutir, refletir, criticar e expor suas opiniões. Assim, com o intuito de fomentar o debate e demonstrar que a implementação da metodologia de Modelagem Matemática pode ser aplicados no ensino fundamental, foi realizado um relato de experiência a partir da exposição de problemas a fim de verificar a viabilidade da aplicação dessas tendências em resolução de problemas e modelagem matemática nesse nível de ensino.

Participaram dessa experiência alunos de uma turma do 9º ano do Ensino Fundamental de uma escola pública do Estado do Piauí, localizada no município de Angical, no Piauí. A sala de aula onde ocorreu o trabalho possuía 22 alunos matriculados e o trabalho se desenvolveu durante as aulas de Matemática ao longo do terceiro bimestre.

O início do trabalho partiu com base no conteúdo do bimestre que foi Probabilidade e Estatística que, após a exposição do conteúdo de probabilidade, percebeu-se a necessidade de repensar como seria feito para explicar o assunto de estatística. Após alguma reflexão, o educador-pesquisador decidiu iniciar a exposição do conteúdo utilizando-se de situações problemas, de modo a integrar Matemática e Ciências, através das seguintes questões-problemas: (1)Quais as doenças mais comuns na comunidade? (2)E com que frequência elas ocorrem? Será que existem pessoas da população com problemas graves de saúde?

Ao expor essas perguntas, muitos alunos questionaram qual seria a relação com a disciplina de Matemática. Explicou-se, então, que é possível correlacionar através da quantificação dos casos de doenças mais comuns, podendo expressar esses dados através de porcentagem, gráficos, tabelas e etc.

Após a explicação dessa correlação a turma foi dividida em equipes e cada equipe iria pesquisar sobre o assunto. Segundo os autores, um ponto interessante a ser observado foi a participação maciça dos alunos e o seu envolvimento com o trabalho, não pelo fato de valer uma nota mas por ser algo que chamou a atenção deles.

No primeiro momento do desenvolvimento da atividade foi realizada uma pesquisa de modo a buscar as doenças mais frequentes como gripe, dengue, doenças cardiovasculares, etc. Nesse momento, uma dúvida surgiu entre os alunos: Como coletar os dados para a pesquisa? Outra questão também foi levantada: Onde seriam buscados esses dados?

Após pesquisar sobre o assunto, se chegou à conclusão de que os dados poderiam ser encontrados no Hospital da Cidade, nos postos de atendimento e na Secretaria de Saúde do município. Com a intervenção do educador-pesquisador, na fase de coleta dos dados, os alunos optaram por utilizar um questionário. Outras dúvidas surgiram na construção do instrumento de coleta, como: Quais as faixas etárias que ocorre maior número de casos de doenças? Qual o gênero em que esses casos são mais frequentes? Existe alguma região da cidade onde esses casos ocorrem com maior frequência?

Esses questionamentos foram acrescentados no questionário. Após, o questionário foi aplicado, não sendo esclarecido os responsáveis pela aplicação no relato, e os dados foram expostos em sala de aula, onde, juntamente com o educador, foi feita a tabulação e a representação gráfica dos resultados. Com os resultados, foi possível trabalhar com os alunos questões que envolviam média, mediana, moda, além de porcentagem, regra de três, operações aritméticas e construção de gráficos.

O objetivo, além de ensinar os conteúdos, foi mostrar que a matemática é uma ciência que ajuda a compreender a sociedade por meio da análise e interpretação de dados de problemas reais. Os alunos gostaram dessa forma de trabalho, uma vez que eles participaram de forma ativa durante todo o processo de construção do conhecimento. Apesar que em alguns momentos foi necessário a intervenção do educador no intuito de manter o controle das discussões.

Com essa experiência, os pesquisadores relatam que foi possível observar que trabalhar com a metodologia de Modelagem Matemática é sempre um desafio, pois exige do educador a capacidade para saber quando e quanto deve ajudar os alunos, além da “tensão do próximo passo” pelo fato de “lidar com situações imprevisíveis”. George Polya (1997, p.3) dá uma indicação a este respeito:

“[...]se o professor auxilia seus alunos apenas o suficiente e discretamente, deixando-lhes alguma independência ou pelo menos alguma ilusão de independência, eles podem se inflamar e desfrutar a satisfação da descoberta”.

Durante a realização desse trabalho, observou-se que as atividades em grupos foram as que mais tiveram a participação dos alunos e isso contribuiu para a aprendizagem dos mesmos frente às negociações necessárias na vida em sociedade. Desta forma, o educador deve ocupar uma posição de mediador entre o conhecimento e o aluno e fazer com que os alunos busquem o entendimento de forma ética.

O trabalho expõe uma experiência com alunos da Rede Municipal de Ensino de Porto Alegre/RS, sob a ótica da Educação Estatística e com a utilização da Modelagem Matemática enquanto estratégia metodológica e inspirados nos princípios da Educação Crítica. O relato apresenta conceitos essenciais para sua compreensão da Educação Estatística e a vinculação dela à Modelagem Matemática de modo a colaborar com seu desenvolvimento.

A experiência relatada foi desenvolvida com 25 alunos do Terceiro Ano do Terceiro Ciclo de uma Escola Municipal de Porto Alegre/RS, os quais foram convidados a realizar uma atividade de modelagem matemática, por meio da qual buscou-se desenvolver as competências estatísticas e as relações e reflexões sociais provindas da metodologia utilizada. Para apoiar esse desenvolvimento, os alunos trabalharam com a temática “Gênero e Sexualidade”, que também colaborou para a formação crítica social dos indivíduos.

Ao longo de cinco aulas, totalizando 400 minutos, foi realizada a prática pedagógica. Inicialmente, os alunos foram questionados se conheciam a comunidade escolar (professores, funcionários, alunos e pais). A partir da negativa, os alunos descreveram o perfil da comunidade escolar em algum aspecto que tivessem curiosidade. Os alunos foram separados em grupos e escolheram o tema “sexualidade”. Esse tema foi mais especificado a partir de um debate entre os alunos acerca da abrangência do tema, de modo que dentro do tema inicialmente proposto, se definiu que o subtema seria “orientação sexual”.

Os alunos trouxeram perguntas e questionamentos os quais foram transcritos na lousa para visualização de toda turma. Selecionadas as perguntas, foi realizada uma breve explicação sobre conceitos básicos relacionados ao tipo de pesquisa que seria realizada, apresentando os conceitos de população e amostra, além da classificação das variáveis a serem obtidas quanto ao tipo (qualitativas - nominais e ordinais - e quantitativas - discretas e contínuas).

A dúvida quanto à orientação sexual teve que ser melhor investigada pelos alunos, pois houve dificuldade no entendimento. Assim, os grupos foram orientados a realizar uma pesquisa em casa sobre como se define a orientação sexual de um indivíduo. Após algumas discussões e esclarecimentos, foi consenso da necessidade das seguintes alternativas constarem no questionário: heterossexual, homossexual, bissexual, assexual e pansexual.

Foi realizada uma categorização das perguntas para que o questionário fosse finalizado. Os alunos foram orientados a realizarem as entrevistas em duplas ou trios, sempre com um único entrevistador e os demais realizando a anotação das respostas, tendo a possibilidade de, quando autorizados, realizarem a gravação das entrevistas.

Após a coleta de dados realizada, foi solicitado aos grupos que discutissem estratégias de organização das respostas obtidas nas entrevistas, relatando a discussão de forma escrita ou através da gravação da discussão realizada. Para isso, o professor circulou entre os grupos, explicando a atividade, evitando dar sugestões de organização, justamente buscando com que os alunos fizessem o debate sobre as possibilidades existentes.

Quando as primeiras ideias surgiam, o professor se afastava, incentivando a discussão e a organização das respostas. Era sempre necessário salientar aos alunos que fizessem os registros dos diálogos para entrega posterior dos relatórios de discussão. Os alunos foram orientados, após concluírem suas discussões, a participar de uma socialização, onde foram as propostas foram apresentadas e debatidas quanto à organização dos dados.

Dos seis grupos, quatro se manifestaram com a unificação das respostas por pergunta (na qual redigiram as perguntas ordenadamente e as respostas de cada um dos entrevistados expostos em lista) e um grupo não chegou a um consenso da organização. Já o último grupo fez considerações quanto aos tipos de respostas possíveis (questões abertas e fechadas), a categorização das questões abertas para auxiliar na organização destas e a contagem de frequência para a construção de gráficos. Houve a explicação acerca da tabulação e representação gráfica dos dados, inclusive no que diz respeito aos tipos de gráficos e seu uso adequado para cada tipo de variável. Encerrada a discussão, os alunos foram convidados a expor as organizações propostas como etapa final da pesquisa e entregar num formato de relatório.

Percebe-se que a maior parte (quatro de seis grupos) apresentaram competências aquém das esperadas pela etapa de ensino, como podemos perceber no registro do Grupo 1, ao apresentarem uma estratégia de organização primitiva de organização dos dados, relatando que “[...]a gente pode colocar o número 1 [relativo à questão 1] e anotar a resposta de todo mundo,[...] e faz isso para cada pergunta”. Em contraponto a essa situação, um dos grupos relata que a ideia foi “[...]de fazer um gráfico com as respostas de sim, não, talvez, não sei, respostas fechadas [...]". Pensamos também em um cartaz dividindo [as respostas abertas] em três partes com as respostas positivas, negativas e neutras”.

Esse relato expõe um desenvolvimento de competências estatísticas de letramento e raciocínio estatísticos elaborados, com número maior de possibilidades de organização e estruturação de apresentação de dados, apesar de não apresentar explicitamente a organização por tabela de frequência, esperada para a construção dos gráficos. Nas discussões realizadas na fase de construção do instrumento de coleta de dados, percebeu-se a evolução da percepção relacionada ao objetivo delimitado pelo grupo em relação às perguntas inseridas na entrevista, o que evidencia a criticidade projetada para a atividade.

Ademais, as discussões proporcionadas acerca da temática “gênero e sexualidade” expuseram as diversas opiniões existentes naquele grupo, além de promover debates relacionados aos discursos de ódio.

Com o objetivo de examinar resultados decorrentes da exploração de atividades envolvendo Modelagem Matemática e o tema esporte, além de identificar e averiguar relações matemáticas existentes neste tema a partir das ações realizadas com os estudantes, a intervenção pedagógica relatada apresenta algumas atividades realizadas com alunos de uma turma de 6º ano do Ensino Fundamental. O artigo não cita a quantidade de alunos envolvidos na dinâmica. Sabe-se que foram entrevistados 41 pessoas do 8º e 9º ano do ensino fundamental.

Os autores preconizam que o papel do educador é orientar os estudantes para que suas ideias ou problemas possam ser expressos matematicamente. Assim, essa atitude pode ser vista como uma forma de o professor controlar as ações do estudante, conduzir sua conduta, tornando-o corresponsável pela aprendizagem e interessado pela matemática escolar. As ações efetivadas tiveram o objetivo de desenvolver uma proposta com foco na Modelagem Matemática como metodologia de ensino, utilizando o tema de interesse dos estudantes.

Inicialmente, foi necessário que os alunos escolhessem um tema. Por meio de entrevistas prévias, foi identificado a preferência pelo tema “esporte”. No primeiro dia de intervenção, a pesquisadora questionou os alunos sobre o que eles entendiam sobre esporte, quais modalidades praticavam e o que mais gostavam nas aulas de educação física na escola.

A partir das respostas, foi proposto à turma a elaboração de um questionários que seria utilizado para entrevistar outros alunos. Na medida que a turma criava as perguntas, estas eram expostas no quadro para que todos pudessem analisá-las. Ao final da explanação, em conjunto, os alunos escolheram as que fariam parte do questionário, além de ordená-las para as entrevistas.

No segundo encontro, de posse das entrevistas realizadas, iniciou-se a tabulação dos dados em quadros, os quais apresentavam o número de respostas obtidas em cada pergunta. Foram confeccionados sete quadros, um para cada pergunta, os quais, em seguida, foram convertidos em gráficos de barras. Após o término da construção de todos os gráficos, um para cada pergunta, a turma foi indagada sobre como poderiam representar os dados e se lembravam ter aprendido algum tipo de número que pudesse representar tais quantidades. Como última atividade do dia, os alunos foram estimulados a representarem as frações em forma de porcentagem. A pesquisadora precisou mostrar o cálculo da transformação, tendo em vista que alguns estudantes não lembravam como realizá-lo. os alunos decidiram em conjunto que seria utilizada apenas uma casa após a vírgula. Para realizarem a interpretação dos gráficos e valores obtidos na tabulação dos dados, os estudantes foram incentivados a elaborarem frases para representar o que eles haviam observado em cada questão.

Ao analisar o texto pode-se observar a percepção dos estudantes diante das informações coletadas nas entrevistas, além das justificativas apresentadas pela maioria. Como por exemplo, a popularidade do futebol e o sábado como dia mais propício a prática de esportes, por ser um dia de “folga” para a maioria das pessoas.

As atividades realizadas à luz da Modelagem Matemática, apresentada neste relato, proporcionou aos alunos uma relação diferenciada com a matemática. Ou seja, os estudantes utilizaram a temática do esporte para elaborar perguntas que consideravam interessantes para compor o questionário, bem como realizar as entrevistas e ainda tabular e analisar o que os resultados apresentavam. Isso possibilitou aos educandos vivenciar o estudo de conceitos matemáticos sem a necessidade da resolução de exercícios formais, como por exemplo, em números fracionários e porcentagem.

Cabe ainda expor percepções gerais sobre a metodologia da Modelagem Matemática e o papel do professor. Ao realizar atividades com os estudantes a partir de um tema de interesse, o papel da professora pesquisadora foi de questionadora e orientadora. Durante a elaboração do questionário, a função da docente foi de instigar os estudantes a determinar que pergunta seria interessante apresentar para seus entrevistados.

ALMEIDA, L. M. W. de; FERRUZZI, E. C. Uma aproximação socioepistemológica para a modelagem matemática. Alexandria: Revista de Educação em Ciência e Tecnologia, v. 2, n. 2, p. 117-134, 2009.

BARBOSA, J. C. Modelagem na Educação Matemática: contribuições para o debate teórico. In: REUNIÃO ANUAL DA ANPED, 24., 2001, Caxambu. Anais... Rio Janeiro: ANPED, 2001. 1 CD-ROM.

BATANERO, C. Didáctica de la Estadística. Granada: Universidad de Granada, 2001. 210 p.

BIEMBENGUT, M. S. 30 Anos de Modelagem Matemática na Educação Brasileira: das propostas primeiras às propostas atuais. ALEXANDRIA: Revista de Educação em Ciência e Tecnologia, v. 2, n. 2, p. 7-32. 2009. Disponível em: https://periodicos.ufsc.br/index.php/alexandria/article/view/37939/28967. Acesso em: 20 abr. 2019.

__________. Concepções e Tendências de Modelagem Matemática na Educação Brasileira. Cuadernos de Investigación y Formación en Educación Matemática, ano 7, n. 10, p. 195-204, 2012.

BIEMBENGUT, M. S.; HEIN, N. Modelagem Matemática no Ensino. 3. ed. São Paulo: Contexto, 2003.

BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática (1º e 2º ciclos do ensino fundamental). v. 3. Brasília: MEC, 1997.

BRASIL. Ministério da Educação. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais (Ensino Médio). Brasília: MEC, 2000.

BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Base Nacional Comum Curricular: Ensino Fundamental. Brasília: MEC, 2017.

CALDEIRA, A. D.; SILVEIRA, E.; MAGNUS, M. C. M.. Modelagem Matemática: alunos em ação. In: Práticas de modelagem matemática: relatos de experiências e propostas pedagógicas. Londrina: Eduel, p. 65-81, 2011.

CAMPOS, C. R. A educação estatística: uma investigação acerca dos aspectos relevantes à didática da estatística em cursos de graduação. 2007. 242 p. Tese (doutorado) - UNESP, Rio Claro (SP), 2007. Disponível em: https://repositorio.unesp.br/bitstream/handle/11449/102161/campos_cr_dr_rcla.pdf?sequence=1&isAllowed=y. Acesso em: 11 set. 2018.

CAMPOS, C. R.; WODEWOTZKI, M. L. L; JACOBINI, O.R; FERREIRA, D. H. Educação Estatística no Contexto da Educação Crítica. Boletim de Educação Matemática - BOLEMA. Rio Claro, v. 24, n. 39, p. 473-494, 2011. Disponível em: http://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/5104/4015. Acesso em: 04 jan. 2017.

CAMPOS, C. R.; WODEWOTZKI, M. L. L; JACOBINI, O.R. Educação Estatística: teoria e prática em ambientes de modelagem matemática. 2. ed. Belo Horizonte: Autêntica, 2013.

CHANCE, B. L. Components of statistical thinking and implications for instruction and assessment. In: Journal of Statistics Education, v. 10, n. 3., 2002. Disponível em: http://www.amstat.org/publications/jse/v10n3/chance.html. Acesso em: 25 mar. 2019.

FIORENTINI, D. Formação de professores a partir da vivência e da análise de práticas exploratório-investigativas e problematizadoras de ensinar e aprender matemática. Cuadernos de Investigación y Formación en Educación Matemática, Costa Rica, Ano 7, n. 10, p. 63-78, 2012. Disponível em: http://revistas.ucr.ac.cr/index.php/cifem/article/view/10560/9997. Acesso em: 04 jan. 2017.

GAL, I. Adults Statistical Literacy: meanings, components, responsibilities. International Statistical Review, v. 70, n. 1, 2002.

GAL I. Statistical Literacy. In: The Challenge of Developing Statistical Literacy, Reasoning and Thinking. p. 47-78. Dordrecht :Springer, 2004

GAL, I.; GARFIELD, J. The assessment challenge in statistics education. Amsterdã: IOS Press, 1997.

GARFIELD, J. The statistical reasoning assessment: development and validation of a research tool. In: Proceedings of the fifth international conference on teaching statistics, p. 781-786, International Statistical Institute. Mendoza, Voorburg, Holanda: Ed. L. Pereira, 1998.

GARFIELD, J. The challenge of developing statistical reasoning. In: Journal of Statistics Education, v. 10, n. 3, 2002. Disponível em: http://jse.amstat.org/v10n3/garfield.html. Acesso em: 12 jan. 2019.

GARFIELD, J. B.; GAL, I. Assessment and Statistics Education: Current Challenges and Directions. In: International Statistical Review, v. 67, n. 1, 1999.

HOERL, R. W. Introductory statistical education: radical redesign is hended, or is it?. In: Newsletter for the section on Statistical Education of the American Statistical Association, 1997.

KAISER, G.; SRIRAMAN, B. A global survey of international perspectives on modelling in mathematics education. Zentralblatt für Didaktik der Mathematik, Costa Rica, vol. 38, n. 3, p. 302-310, 2006. Disponível em: http://link.springer.com/article/10.1007/BF02652813. Acesso em: 04 jan. 2017.

MACHADO, M. B.; SANT'ANA, A. A. Modelagem Matemática: ambiente de aprendizagem de conteúdos programáticos de Estatística . In: CIEM - Congresso Internacional de Educação Matemática, 7., 2017, Canoas. Anais... Canoas: ULBRA, 2017. Disponível em: http://www.conferencias.ulbra.br/index.php/ciem/vii/paper/viewFile/7097/3169. Acesso em: 14 jul. 2019

MALLOWS, C. The zeroth problem. In: The American Statistician, 52., p. 1-9, 1998.

MELLO, L. I. P. de; NUNES, L. N. A Matemática abordando a Estatística através de um estudo sobre os óbitos dos escravos no Rio Grande do Sul no século XIX: uma experiência interdisciplinar. In: CIEM - Congresso Internacional de Educação Matemática, 7., 2017, Canoas. Anais... Canoas: ULBRA, 2017. Disponível em: http://www.conferencias.ulbra.br/index.php/ciem/vii/paper/viewFile/6446/3827. Acesso em: 14 jul. 2019

MEMÓRIA, J. M. P. Breve história da estatística. Brasília: Embrapa Informação Tecnológica, 2004. 111p.

MENDES, F. G. L.; SOUSA, B. O. de. A modelagem matemática nos conteúdos do 3º bimestre para o ensino de estatística em uma escola de Angical do Piauí. In: CONEDU - Congresso Nacional de Educação, 4., 2017. Anais IV CONEDU... Campina Grande: Realize Editora, 2017. Disponível em: https://editorarealize.com.br/artigo/visualizar/35477. Acesso em: 14 jul 2019

MOORE, D. Teaching statistics as a respectable subject. In: Statistics for the twenty-first century, The Mathematical Association of America, p. 14-25. Washington DC: F. and S. Gordon, 1992.

MOORE, D. S. Foreword. In: BEN-ZVI, D.; GARFIELD, J. (Eds.). The Challenge of Developing Statistical Literacy, Reasoning and thinking. Dordrecht, The Netherlands: Kluwer Academic Publishers, 2004, p. ix-x.

NISBETT, R. Rules for reasoning. Mahwah, NJ: Lawrence Erlbaum, 1993.

PFANNKUCH, M. & WILD, C. Towards an Understanding of Statistical Thinking. In: The Challenge of Developing Statistical Literacy, Reasoning and Thinking, p. 17-46. Dordrecht, Holanda: Kluwer Academic Publishers, 2004.

RUMSEY, D. J. Statistical Literacy as a goal for introductory Statistics courses. In: Journal of Statistics Education, v. 10, n. 3., 2002. Disponível em: http://jse.amstat.org/v10n3/rumsey2.html. Acesso em: 25 mar. 2019.

SANTOS, R. M. dos. Estado da arte e história da pesquisa em educação estatística em programas brasileiros de pós-graduação. 2015. 348 p. Tese (doutorado) - UNICAMP, Campinas (SP), 2015. Disponível em: http://www.repositorio.unicamp.br/bitstream/REPOSIP/305010/1/Santos_RodrigoMedeirosdos_D.pdf. Acesso em: 11 set. 2018.

SCHWANCK, D. I.; NUNES, L. N. Educação Estatística e Modelagem Matemática: reflexão sobre uma prática na Rede Municipal de Porto Alegre. In: CIEM - Congresso Internacional de Educação Matemática, 7., 2017, Canoas. Anais... Canoas: ULBRA, 2017. Disponível em: http://www.conferencias.ulbra.br/index.php/ciem/vii/paper/viewFile/7147/3955. Acesso em: 14 jul. 2019

SEDLMEIER, P. Improving statistical reasoning: theoretical models and practical implication. Mahwah, NJ: Springer Verlag, 1999.

SILVEIRA, E. Modelagem matemática em educação no Brasil: entendendo o universo de teses e dissertações. 2007. 197 p. Dissertação (Mestrado em Educação), UFPR, Curitiba (PR), 2007.

SKOVSMOSE, O. Cenários para Investigação.Tradução de Jonei Cerqueira Barbosa. In: Boletim de Educação Matemática - BOLEMA. Rio Claro, v. 13, n. 14, p. 66-91, 2000. Disponível em: http://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/10635/7022. Acesso em: 04 jan. 2017.

__________. Educação matemática crítica: a conquista da democracia. 3. ed. Campinas: Papirus, 2001.

SNEE, R. D. Discussion: development and use of statistical thinking: a new era'. In: Internacional Statistical Review, 67., p. 255-258, 1999.

WILLCOX, W. F. The Founder of Statistics. Revue De L'Institut International De Statistique / Review of the International Statistical Institute, v. 5, n. 4, 1938, p. 321–328. Disponível em: www.jstor.org/stable/1400906. Acesso em: 02 mai. 2019.

ZIEGLER, J. de R.; QUARTIERI, M. T. Uma intervenção pedagógica com alunos do 6º Ano do Ensino Fundamental à luz da Modelagem Matemática. In: CIEM - Congresso Internacional de Educação Matemática, 7., 2017, Canoas. Anais... Canoas: ULBRA, 2017. Disponível em: http://www.conferencias.ulbra.br/index.php/ciem/vii/paper/viewFile/7410/3203. Acesso em: 14 jul. 2019