


O sr. Poincaré dá a explicação seguinte. A concepção que temos de espaço tem por base uma imagem que se forma sobre nossa retina e que tem duas dimensões. A ideia de uma terceira dimensão resulta do esforço de acomodação que é preciso fazer com nossos olhos e da convergência que é preciso lhes dar; ela depende dessas duas indicações que são distintas, mas que sempre se encontram concordantes e equivalentes assim a uma só. Aqueles elementos de nossas sensações visuais que concorrem para formar em nós a noção do espaço são então, em definitivo, funções de três variáveis independentes, e é daí que viria o sentimento de três dimensões. Concebemos, de resto, a possibilidade de um estado de coisas tal que as duas indicações que constituem juntas a terceira variável sejam independentes uma da outra, ao invés de serem ligadas entre si por uma relação constante; então atribuiremos sem dúvida quatro dimensões ao espaço visual.
Eis uma outra explicação, de Hinton.
O analista pode, ou ao menos pôde até nossos dias, interpretar os fenômenos da Natureza com a seguinte concepção de espaço. Para ele, este não deve ser outra coisa do que um Sistema de três variáveis, que ele chama de distâncias ou coordenadas,[2] e às quais demanda unicamente poder tomar todos os valores imagináveis, cada um independentemente dos dois outros; um ponto do espaço é para ele apenas um sistema de valores determinados dessas três variáveis, e o conhecimento do mundo material aquele das relações que têm entre elas e com o tempo, em um certo conjunto de circunstâncias chamado de fenômeno. É sobre essa base que foram edificados os imortais trabalhos de Laplace, Lagrange, Poisson, ..., etc.
Três variáveis, eis então a que se reduzem, no final das contas, e combinando seus efeitos, as mil e uma causas que existem em torno de nós e que engendram tudo o que nos faz ter alegria ou sofrimento. Talvez seja muito simplesmente esse fato que, sentido confusamente pelo espírito de nossos pais, ali tenha se fixado, ao longo do tempo, sob a forma mais ou menos gratuita de uma coisa chamada espaço e dotada de três dimensões, de resto bastante imprecisas: por uma de suas operações favoritas, o dito espírito teria substituído essa coisa concreta pelo sistema analítico abstrato.
Esse não seria o único caso no qual teríamos visto o instinto popular ultrapassar o matemático; vejamos, por exemplo, o que se diz sobre o tema dos “Treze à mesa” nos Contes de la veillée, de Charles Nodier e, pelo sr. Dormoy, no Journal des Actuaires français, fascículo de janeiro de 1875, p. 62.
Ora, ocorre que as três variáveis não são suficientes para a Análise uma vez que, cada vez mais poderosa e exigente, ela levou suas pesquisas ao mundo das pequenas dimensões, que nossos pais ignoravam; a razão dessa insuficiência é que um estudo mais aprofundado nela descobre efeitos cujas causas eram até então inexistentes. Desde então ela é levada, por bem ou por mal, a substituir para esses novos estudos seu sistema de três variáveis por um de quatro. Veremos mais adiante [3] que a quarta, que intervém apenas a propósito de três pequenas grandezas e de três pequenos movimentos, traduz-se, concretamente, por uma quarta espessura muito pequena. Quanto mais minucioso se tornar o estudo da Natureza, mais será necessário, como nos Métodos de aproximações sucessivas, aumentar o número das variáveis e, por conseguinte, aquele das dimensões espaciais, ao menos na ordem de pequenez considerada.
Se essa segunda explicação é a boa, não poderia se produzir progressivamente, em nossa mentalidade que lida com causas cada vez mais numerosas, uma transformação correspondente àquela da Análise, tendo por resultado dar a nossos distantes descendentes a sensação de se ver, e de conceber o espaço, com quatro dimensões?
O geômetra concebe o espaço dividido em uma infinidade de fatias infinitamente finas que ele chama de planos, estes em uma infinidade de faixas infinitamente estreitas que ele chama de retas, e estas em uma infinidade de segmentos infinitamente curtos que ele chama de pontos. Por vezes o que ele chama de planos, retas e pontos, são não as fatias, as faixas e os segmentos em si, mas as separações, desprovidas de qualquer espécie de espessura e de realidade, que seu pensamento vê entre eles. Essas divisões ou essas separações, ele faz delas tanto seres particulares, que afasta uns das outros, com ou sem as coisas que contêm; ele os desloca de todos os modos e os entrecruza a seu bel prazer; ele os povoa de figuras criadas por sua imaginação, ligadas entre si pelas leis das quais ele mesmo se torna escravo. Seguindo uma ou outra maneira da concepção dessas espécies de tabiques, triângulos e bolinhas que se formou nele, ele diz que em três dimensões há uma infinitamente pequena junto aos planos, duas junto às retas, três junto aos pontos, ou ainda que ao invés de terem três dimensões, os planos têm apenas duas, as retas apenas uma, e os pontos não as têm. De todo modo, as divisões são puramente ideais, e podem ser feitas de uma infinidade de maneiras.
Tomando a série em sentido inverso, isto é, a partir do ponto, a geometria que vai nos ocupar a leva mais longe do que o espaço.
Este não passa igualmente para ela de uma fatia (não podemos mais diversificar as palavras e colhemos a última deixada pela série começada), de uma fatia infinitamente fina em meio a uma infinidade de outros espaços que formam outras tantas fatias paralelas em uma extensão de quatro dimensões. Espaços que por sua vez o geômetra povoa, desloca, entrecruza como quer.
Nós chamaremos de EXTENSÃO o conjunto formado por esses espaços em número infinito, e que é seu continente como cada um deles é o continente de uma infinidade de planos, cada um deles o continente de uma infinidade de retas, cada uma delas o continente de uma infinidade de pontos. Nada impede de considerar a extensão como sendo englobada, por sua vez, em um campo de cinco dimensões, e assim outra vez, indefinidamente.
Tal é a concepção dos campos sucessivos. Cada campo procede do precedente por uma amplificação cada vez mais grandiosa. Infinitamente grande em relação a este, ele é infinitamente pequeno em relação àquele no qual está englobado; sem limites segundo cada uma das dimensões das quais está dotado, ele não é mais do que uma coisa evanescente segundo uma última que lhe falta e que existe fora dele.
Que são as coisas que contêm esses campos sucessivos?
Tomemos, para começar, um dos inúmeros planos que nosso pensamento pode criar, acabamos de ver de que modo: esse será, por exemplo, o plano horizontal sobre o qual caminhamos, suposto indefinidamente prolongado em todos os sentidos. As coisas que estão nesse plano não passam de secções feitas por ele através dos corpos em três dimensões, que ocupam o espaço no qual ele se prolonga, ou antes as faces de contato, os afloramentos desses mesmos corpos com o plano. Concebemos ainda aí figuras que não têm essa origem, formadas de linhas e de pontos; mas essas, como seu nome o indica e como o próprio plano, existem apenas em nosso pensamento, por uma abstração da terceira dimensão à qual certos cérebros não se habituam com facilidade.
Todos essas coisas, intersecções, afloramentos ou figuras, podemos conceber se deslocando e se transformando no plano sem restrições nem limites. Mas as concebemos apenas com as duas dimensões deste; no sentido da terceira dimensão, elas têm, como ele, apenas uma espessura, ou nula, ou infinitamente pequena, quer seja o plano concebido conforme uma ou outra das duas maneiras indicadas no começo. Enfim, elas não são seres reais, qualidade que é o apanágio dos corpos em três dimensões.
O que o plano é no espaço, admitimos que o espaço é, por sua vez, na extensão das quatro dimensões: ele é ali, na presença da quarta, como uma fatia (?) infinitamente fina e absolutamente plana, como um plano (?) que seria infinito segundo três dimensões ao invés de o ser segundo duas somente. As mesmas condições deveriam ser concedidas aos seres que ele contém. Em todos, a quarta dimensão é nula ou infinitamente pequena. Aqueles que não são figuras evocadas por nosso pensamento serão as intersecções ou os afloramentos do espaço com corpos em quatro dimensões que existem fora dele, em meio a seres análogos disseminados na extensão em quatro dimensões. Esses últimos gozarão sozinhos da existência real; todos os outros, aqueles que têm três dimensões, ou os sólidos, aqueles que têm duas, ou as superfícies, aqueles que têm apenas uma, ou as linhas, enfim, aqueles que não as têm, ou os pontos, serão, como se diz em filosofia, seres de razão, isto é, abstrações que existem apenas em nosso pensamento. Eles poderão se deslocar e se transformar no espaço sem restrições nem limites (desta vez, é de propósito que repetimos as mesmas expressões), mas eles terão apenas, como ele, uma espessura nula ou infinitamente pequena no sentido da quarta dimensão. Eles ali estarão na superfície [4] para um olho que olhasse o espaço como podemos olhar o plano que está sob nossos pés.
Além disso, o espaço não mais será uma coisa absoluta, uma entidade única e necessária, mas uma simples unidade em meio a uma infinidade de outras, e será necessário dizer: nosso espaço, para especificar aquela das unidades que nos cabe. Que sejam concebidos vazios de qualquer coisa, ou, como o nosso, povoados de universo, nosso espírito não pode a priori formular nenhuma razão nem a favor, nem contra a existência desses espaços congêneres do nosso, nem a favor, nem contra a vasta extensão que tudo abraça. A observação tampouco oferece algo sobre isso. Pareceria então que este tema teria interesse apenas para o geômetra ou para o metafísico; veremos, contudo, que pode ser de outro modo, e que esses outros espaços, que com o nosso formam uma única e mesma coisa, que têm com ele a mesma continuidade que os planos de um espaço têm entre si, podem, apesar das aparências, não ser para eles completamente estrangeiros, e explicam muitas das grandes dificuldades às quais se furtam as ciências físicas.
É neste sentido, para tornar a nossas primeiras palavras, que pertencemos ao mundo das quatro dimensões, se ele existe. E, se ele existe, está submetido às leis da Geometria que nós iremos esboçar, como o nosso está submetido, com os pequenos campos que engloba, àquelas da Geometria comum.
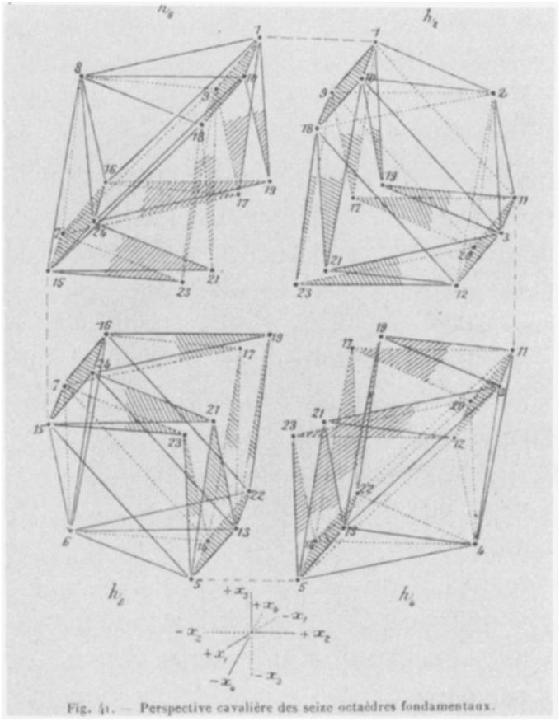
Perspective Cavalière.
E. Jouffret, Traite elementaire de geometrie a quatre dimensions
Paris, 1903.
_______________________
[1] Fonte: JOUFFRET, E. Avant-Propos. In: _____. Traité Élémentaire de Géométrie à quatre dimensions et introduction à la géométrie à n dimensions. Paris : Gauthier-Villars, Imprimeur-Libraire, 1903. p. VI-XII. Trad. Daniela Kern.
[2] Sua significação absoluta a ele importa pouco e pode mesmo mudá-la sob certas condições; cf. § 17, 18 e 19. N. A.
[3] No final do Prefácio e no § 48. N. A.
[4] Essa imagem será apresentada de modo preciso no final do Prefácio. N. A.